Comprendre le mouvement des astres
Le mouvement dans un champ de gravitation explique la trajectoire des planètes, des satellites, des comètes et de tout corps soumis à l’attraction gravitationnelle d’un astre. C’est à partir de cette force invisible que les scientifiques peuvent prédire le passage d’une comète ou choisir l’altitude d’un satellite. Pour bien saisir ces concepts, il est essentiel de plonger dans les lois de Kepler et la loi de la gravitation universelle.
Les lois de Kepler
La première loi de Kepler : les orbites elliptiques
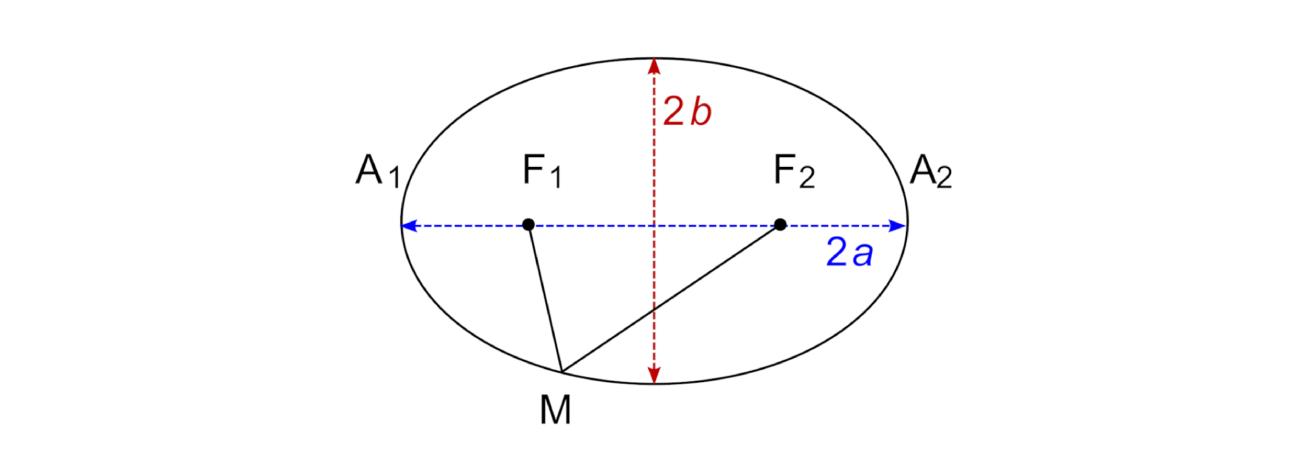
Dans le référentiel héliocentrique, la trajectoire des planètes est une ellipse dont le Soleil occupe l’un des foyers. Une ellipse est une forme étirée du cercle, avec deux foyers distincts.
Quelques points à retenir :
- Périhélie : point le plus proche du Soleil.
- Aphélie : point le plus éloigné du Soleil.
- Pour les satellites autour de la Terre, on parle de périgée et d’apogée.
La majorité des orbites dans le système solaire sont très proches du cercle, mais certaines, comme celles de Pluton ou d’Éris, sont bien plus allongées.
La deuxième loi de Kepler : la loi des aires
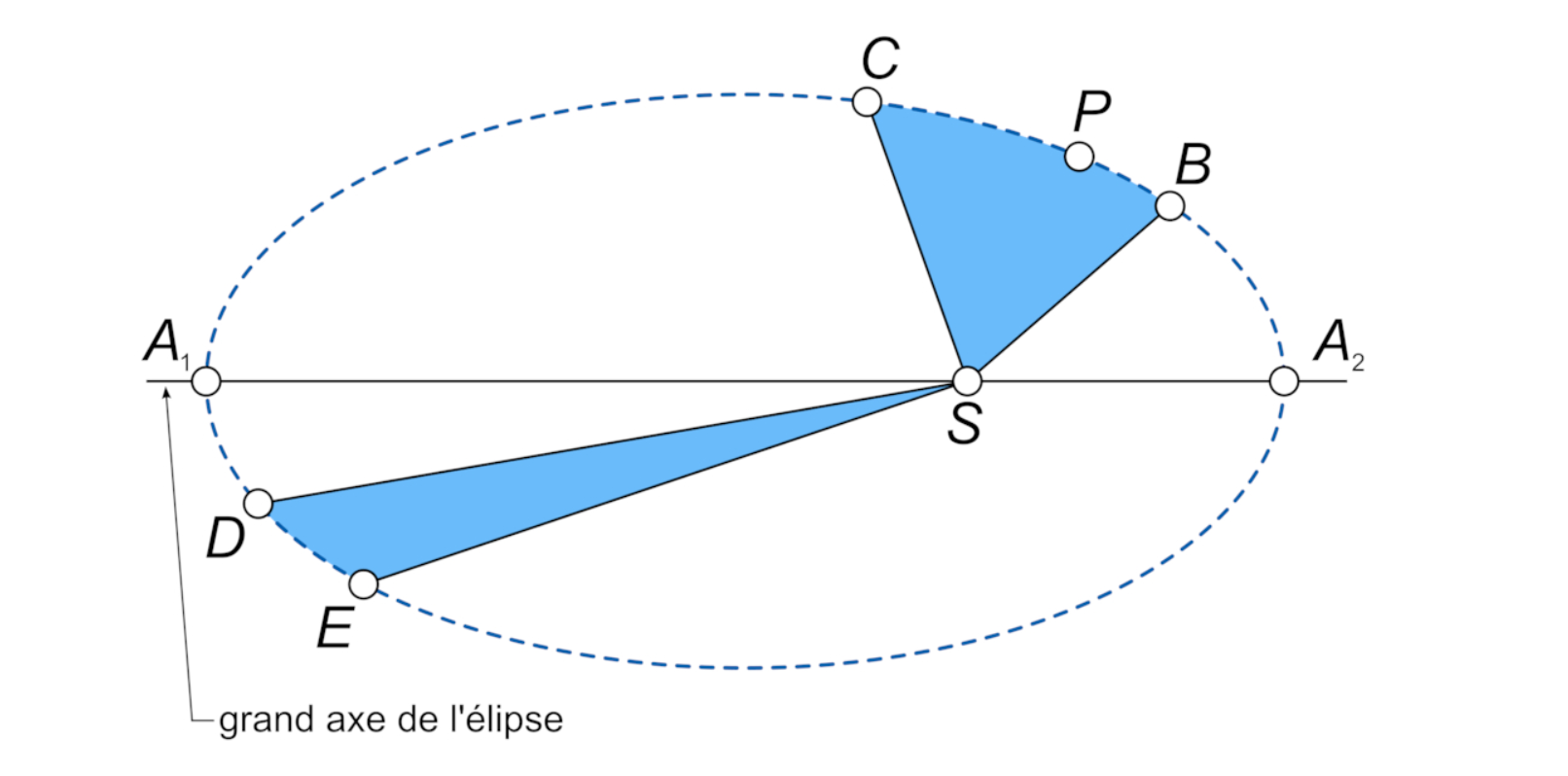
La deuxième loi de Kepler, énoncée en 1609, précise que le rayon reliant une planète à son astre balaie des aires égales pendant des temps égaux.
Concrètement :
- Quand une planète est proche du Soleil, elle va plus vite.
- Quand elle est éloignée, elle ralentit.
Imaginez un grand drap tendu, avec une boule de pétanque au centre pour symboliser le Soleil. Une bille qui passe près de la boule glisse plus vite que lorsqu’elle est loin. C’est cette image qui aide à comprendre l’effet de la gravitation.
La troisième loi de Kepler : la loi des périodes
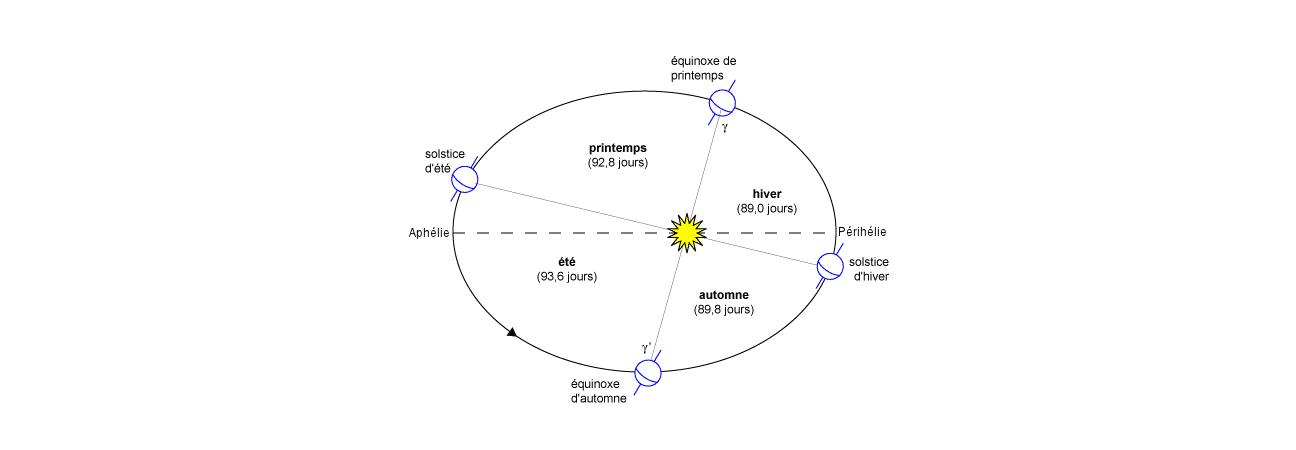
Cette loi, énoncée en 1618, relie la durée d’une révolution à la taille de l’orbite.
Formule simplifiée :
T² ∝ R³
Plus l’orbite est grande, plus la période est longue. Cette loi est indispensable pour positionner correctement les satellites autour de la Terre.
La loi de la gravitation universelle
Isaac Newton a formalisé l’idée que deux masses s’attirent mutuellement. La force exercée par un corps de masse m1 sur un corps de masse m2 est proportionnelle à leur produit et inversement proportionnelle au carré de la distance qui les sépare.
Formule :
F = G × (m1 × m2) / r²
avec :
- F : force gravitationnelle.
- G : constante universelle de gravitation.
- r : distance entre les deux corps.
Analyser un mouvement en orbite
Forces en jeu
Lorsqu’un satellite est en orbite autour d’une planète, la seule force qui agit est la gravitation. Cela veut dire que le satellite est en chute libre permanente, mais sa vitesse tangente à la trajectoire le maintient à distance constante.
Application de la deuxième loi de Newton
Pour un satellite de masse m soumis à l’attraction d’un astre de masse M :
m × a = F
Donc :
m × a = G × (m × M) / r²
Ce qui donne l’accélération :
a = G × M / r²
Cette accélération est centripète, dirigée vers le centre de l’astre.
Vitesse orbitale
En orbite circulaire :
F = m × v² / r
En égalant :
v = √(G × M / r)
La vitesse est donc constante si l’orbite est circulaire.
La période de révolution
La période est le temps pour faire un tour complet de l’orbite :
v = 2πr / T
En combinant :
T = 2π √(r³ / (G × M))
Ce qui correspond exactement à la troisième loi de Kepler.
Les satellites géostationnaires
Définition
Un satellite géostationnaire reste immobile par rapport à un point de l’équateur terrestre. Il tourne à la même vitesse que la Terre tourne sur elle-même.
Conditions à respecter :
- orbite circulaire et équatoriale
- période de révolution de 24 heures
Calcul de l’altitude
En utilisant la troisième loi de Kepler :
r ≈ 42 164 km
Comme la Terre mesure environ 6 378 km de rayon, l’altitude du satellite est donc d’environ 36 000 km.
Utilités des satellites géostationnaires
- Communications (téléphone, télévision).
- Météorologie (images satellites).
- Navigation.
Mouvements des comètes et autres corps
Les comètes comme Halley passent près de la Terre selon des orbites très allongées. Lorsqu’elles sont loin du Soleil, elles avancent lentement ; à l’approche, elles accélèrent fortement sous l’effet de la gravitation.
Les lois de Kepler permettent de prédire précisément leur retour.
La relativité et la gravitation
La théorie d’Einstein montre que la gravitation est une déformation de l’espace-temps causée par les masses.
Cette correction relativiste est indispensable aujourd’hui, notamment pour le fonctionnement précis des satellites GPS.
Points clés à retenir
- La trajectoire d’un corps soumis uniquement à la gravitation est une ellipse.
- En orbite circulaire, le mouvement est uniforme.
- La vitesse orbitale dépend de la masse de l’astre et de la distance.
- Les satellites géostationnaires offrent une couverture constante.