Le théorème de Pythagore est une notion incontournable des mathématiques enseignée dès le collège. Simple dans son énoncé mais puissant dans ses applications, il s’avère utile dans de nombreux domaines. Découvrons ensemble ses principes, ses applications et ses secrets.
Qu’est-ce que le théorème de Pythagore ?
Le théorème de Pythagore établit une relation mathématique fondamentale dans un triangle rectangle. Selon ce théorème, dans tout triangle rectangle, le carré de la longueur de l’hypoténuse (le côté le plus long) est égal à la somme des carrés des longueurs des deux autres côtés.
Formule mathématique
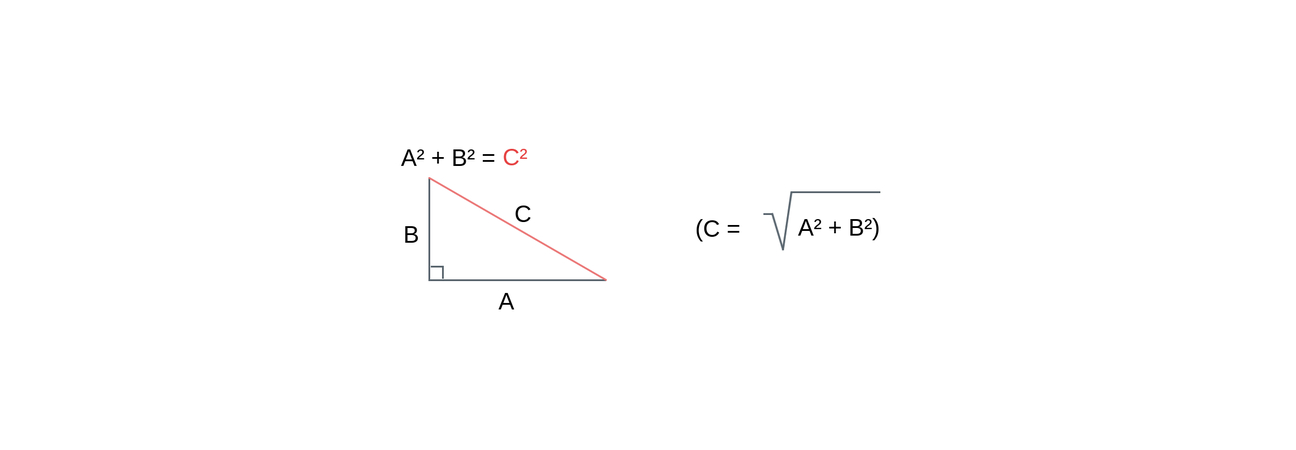
La formule du théorème s’écrit simplement :
a² + b² = c²
Où :
- a et b sont les longueurs des côtés adjacents à l’angle droit,
- c est la longueur de l’hypoténuse.
Application simple
Prenons un exemple. Si un triangle rectangle a des côtés de longueur 3 cm et 4 cm, alors :
Hypoténuse² = 3² + 4² = 9 + 16 = 25
Ainsi, l’hypoténuse mesure 5 cm.
La réciproque du théorème de Pythagore
La réciproque permet de déterminer si un triangle est rectangle. Si le carré de la longueur du plus long côté est égal à la somme des carrés des deux autres côtés, alors le triangle est rectangle.
Exemple pratique
Imaginons un triangle dont les côtés mesurent 6 cm, 8 cm et 10 cm. Vérifions :
Hypoténuse² = 10² = 100
6² + 8² = 36 + 64 = 100
Puisque les deux résultats sont égaux, ce triangle est rectangle.
L’histoire du théorème de Pythagore
Pythagore, philosophe et mathématicien grec, a vécu au VIe siècle av. J.-C. Bien que son nom soit associé au célèbre théorème, il est probable que ce principe mathématique était déjà connu des Égyptiens et Babyloniens.
Les Égyptiens utilisaient une corde avec des nœuds pour construire des angles droits lors de la délimitation des champs. Ces triangles formés par des longueurs de 3, 4 et 5 unités respectaient déjà la formule du théorème de Pythagore.
Lire aussi : qui était Pythagore ?
Les applications du théorème de Pythagore
- En géométrie et en architecture : le théorème est indispensable dans la construction pour vérifier les angles droits et calculer les diagonales. Par exemple, un charpentier peut l’utiliser pour déterminer la longueur d’une poutre diagonale.
- En physique : les lois du mouvement et les vecteurs de force s’appuient souvent sur ce théorème pour décrire les relations spatiales entre objets.
- Dans la vie quotidienne : le GPS utilise des principes basés sur le théorème de Pythagore pour calculer les distances entre des points sur une carte.
Les triplets de Pythagore
Certains ensembles de nombres entiers, appelés triplets de Pythagore, vérifient directement la relation du théorème. Les plus connus sont :
- (3, 4, 5)
- (5, 12, 13)
- (8, 15, 17)
Utilité des triplets
Ces triplets permettent de reconnaître rapidement si un triangle est rectangle sans effectuer de calculs complexes.
Exercices pratiques
Calculer l’hypoténuse
Problème : Dans un triangle rectangle, les côtés mesurent 7 cm et 24 cm. Quelle est la longueur de l’hypoténuse ?
Solution :
Hypoténuse² = 7² + 24² = 49 + 576 = 625
Hypoténuse = √625 = 25 cm
Vérifier si un triangle est rectangle
Problème : Un triangle a des côtés de 9 cm, 12 cm et 15 cm. Est-il rectangle ?
Solution :
Hypoténuse² = 15² = 225
9² + 12² = 81 + 144 = 225
Puisque les résultats correspondent, ce triangle est rectangle.
La démonstration classique du théorème de Pythagore repose sur des constructions géométriques. Par exemple, en traçant un carré et en y insérant des triangles, on prouve que les aires respectent la formule a² + b² = c².
Révisions et astuces
Pour maîtriser le théorème de Pythagore :
- Apprenez par cœur la formule a² + b² = c².
- Entraînez-vous avec des exemples variés.
- Familiarisez-vous avec les triplets de Pythagore pour gagner du temps.
Ce théorème reste une clé pour comprendre la géométrie et résoudre des problèmes du quotidien.
